BASR: Discourse Journal

Teaching and Learning > DISCOURSE

Gardner-Inspired Design of Teaching Materials:A Logical Illustration

Author: Laurence Goldstein and Martin Gough

Journal Title: Discourse

ISSN: 2040-3674

ISSN-L: 1741-4164

Volume: 10

Number: 1

Start page: 173

End page: 202

Return to vol. 10 no. 1 index page

This piece serves as a discussion article based around a project funded by the Higher Education Academy Subject Centre for Philosophical & Religious Studies, entitled 'Design of teaching materials informed by consideration of learning impaired students'.¹ The general aim of this project was fundamentally to re-think the design of teaching materials in the light of what is now known about cognitive deficits and in light of what Howard Gardner has termed 'multiple intelligences', and to construct more effective, more attractive teaching materials as a result. What emerges is certainly not an algorithm but is a suggested recipe for designing innovatory teaching materials that potentially promote deep (as opposed to superficial) learning, and engage the different 'intelligences' of the learner, right across the age spectrum, from nursery to university. This is an important enterprise. The dumbing down of education in the UK means not only that this country is in danger of becoming less competitive internationally, but, more importantly, implies risk that our young people will become trained only in the feeble sort of knowledge-acquisition such as what enables them merely to pick the right answers in simple multiple-choice tests. They would not acquire the love and respect for learning that would make their lives enriched and themselves competitive on the global careers market.

The project aimed to contribute to reversing this sorry decline. In this piece, we describe how the project developed, not only in terms of the generating of findings but also in terms of how more theoretical considerations have come to bear. We consider in the next section how Gardner's framework provides inspiration for this work and consider one of the main critics of his theory. The following section introduces what we term the 'dog-legged' approach to designing teaching tools and materials, how attempting to design new tools to teach learners with a specific impairment provides the clue to alternative tools to teach everyone more effectively. We then discuss what are the important dimensions of 'effectiveness', the deeper rather than the more superficial levels of learning and the more refined 'SOLO taxonomy'.

With the more general and theoretical backdrop established, we can describe the stages specific to the project on the teaching of syllogism, the production of the prototype device (in the section 'Design for the blind: Sylloid') and the device derived from it (in the section 'Sight restored: Son of Sylloid'). Having listed the prima facie advantages and disadvantages of each of the new devices in relation to using Venn diagrams for teaching syllogism, we describe what happened with the testing of Son of Sylloid. The concluding section is able, in light of the testing, to return to the question of what we mean by deep and superficial learning in the context of teaching logic.

What Gardner has to offer

The vehicles of traditional academic learning are principally reading and writing. Knowledge is generally stored in written form (in a variety of media) either in natural language or in an ordinary language supplemented with a specialist vocabulary or in some symbolic system (e.g. the language of mathematics) and is accessed through reading—a wide variety of reading tools are now available to complement our eyes. The knowledge which is encoded in written form paradigmatically is propositional knowledge ('knowledge-that') and there is a considerable philosophical literature on how this kind of knowledge is to be distinguished from 'knowledge-how'. The latter is typically acquired by means other than reading. For example, although there are manuals about flying an aircraft, the relevant know-how is optimally acquired by practice, either in real aircraft or in a flight simulator. Nobody learns to ride a bike just by absorbing a set of instructions. Aresearch question suggests itself: Are there means other than the linguistic (reading and writing) that can profitably replace, in certain areas, traditional means of knowledge acquisition, emphasizing that the areas are more about 'knowledge-how'?

Linguistic intelligence is but one of the several 'intelligences' identified by the psychologist Howard Gardner: the others are logicalmathematical, spatial, bodily-kinaesthetic, musical, interpersonal, intrapersonal and naturalist intelligences, and the pattern of attainment over all of them will vary from one individual to the next. Someone who has good mathematical intelligence, for example, may not be nearly so strong in (say) interpersonal intelligence. To avoid bias towards one of the intelligences, in the sense of directing teaching towards developing and assessing attainment in it, where some learners will already be more proficient in it, it is important to design materials that engage a range of intelligences, thus answering to the diversity of student learning needs. Then, where a student suffers an impairment that inhibits the exercise of one or other of these intelligences (or where a student is just weak in some area), they will not be so disadvantaged in the progress of their learning overall.

There will be limits to this, since some subjects, according to their nature, will have to be understood only in certain ways and not others, at least without in effect changing the nature of the subject in the process. So removing numbers from the study of arithmetic would mean that the result was not arithmetic. But we suggest that there is scope for some creative imagination in devising alternative means to teach a subject within these logical bounds. Just within the linguistic medium, different textbooks appeal to different tastes and different types of learning materials appeal to different talents. A student weak in (say) maths may find the traditional teaching of maths difficult and unappealing. But design a learning task in maths that draws upon (say) a student's talent in music and that student may become instantly engaged and may develop an entirely better attitude to the study of mathematics. Gardner-inspired teaching is now practiced world-wide.

In Mike Fleetham's words:

The theory of multiple intelligences (MI) shows that there is much more to intelligence than high IQ, good spelling or quick mental maths; in fact there's a whole variety of ways to be clever, including musically, verbally, interpersonally, kinaesthetically and naturalistically. MI is a powerful tool that helps you to appreciate and enrich the talents of all your learners, whatever their age. Creating an understanding of MI in schools has been shown to improve pupils' selfesteem, self-motivation and independence, and to help underachievers realize their potential.²

Part of the inspiration for the present project sprang from the success that the first author had in leading a team charged, some fifteen years ago, with the task of producing a bilingual (Cantonese-English) young society in Hong Kong; to bring it about that 30% of secondary school leavers in Hong Kong were genuinely bi-lingual. The scheme was known as the 'Bridge Programme', helping students to cross the bridge from learning in Cantonese to learning in English. The team constructed a suite of texts and audiotapes, in which elements of what students had learned in seven school subject areas using Cantonese as a medium of instruction in their final year of primary school were re-taught and enlarged in the first term of secondary school, with these subjects supplying the content for exercises and activities in English. The design of these communicative exercises and activities was informed by the Gardnerian taxonomy, in that it engaged the different intelligences, giving a student the opportunity to 'shine' in those exercises and activities that called upon the particular intelligences in which he or she is strong.³ Apart from anything else, this gives a tremendous boost to student confidence.

There are controversial aspects of his theory, picked up on by, for instance John White, who questions the rationale, beyond arbitariness, for settling upon just the eight types of intelligence, since there are many more headings describing human action and thought under which we ascribe aptitude. Indeed Gardner is not entirely decided whether he does settle for just eight: his original list numbered seven. Rather than assuming his is the last word on the metaphysics of mind, we are happy, for current purposes at least, to use Gardner as heuristic inspiration for the project and for other ongoing work assuming differences in learning approach, as well as differentials in learning aptitude, by whatever cause, and this is the main point to take forward.⁴

The dog-legged approach to the design of teaching materials

The second source of inspiration for the recent project was a request to construct specialized equipment for teaching elementary logic to blind students. The logic in question was the theory of syllogisms, and one standard method for testing syllogistic arguments for validity is to use diagrams named after their inventor, the 19th century logician John Venn. It hardly needs to be pointed out that the Venn-diagrammatic technique is unavailable to a blind student—someone who in Gardnerian terms is deficient in the visual dimension of spatial and other 'intelligences'—so a substitute apparatus needs to be invented that taps into a different dimension of the 'intelligences' of the blind person. And then the question arises as to whether this apparatus, or some successor of it that re-engages with the visual, will provide a richer learning experience for non-impaired users. If it does then one can reasonably expect this dog-legged design process to be just as applicable, in generalized terms, to other areas of learning.

Let us elaborate just a little. The problem of designing teaching equipment tailored to the needs of a group of individuals whose access to certain modes of learning is restricted, for example because of impairment or weakness in one or other 'intelligence', ought to confront designers with the challenge fundamentally and creatively to re-think questions such as 'What is the real nature of what is being taught (and why is it important, if it is, that it be taught at all)?' and 'What type of learning experience will best promote real, deep understanding of the subject matter?'. Such questions, when addressed seriously, inform the design of the new equipment and so benefit the target users. But the pedagogically important consideration is this: If the piece of equipment is a sophisticated solution to educational questions that have not previously been raised, then it will supply a superior means of learning not just for the group for whom it was designed, but for all students. And this will be true right through the age spectrum. The equipment will, however, typically need to be reconfigured so that a learner who is not restricted is not disadvantaged. For example, if braille letters are used in a device designed for blind subjects, then the braille would be replaced by standard letters or some other visible substitute in versions of the device to be used by the non-blind. And the reconfigured apparatus could also, for example, make effective use of colour. In summary, the dog-legged design process is this:

Identify some part of the syllabus that is taught by some traditional means, e.g. by book learning, where you feel the traditional teaching methods to be stodgy or ineffective. One relevant sense of lack of effectiveness might be that the students' learning tends to be of a 'surface', or superficial, nature.
Construct learning material X (it may be a piece of apparatus, a competitive or collaborative activity for two or more students, an interactive computer game, etc.) for a target group of students that suffers some real or imaginary cognitive deficit. The use of X will engage a range of intelligences different from that invoked by the traditional teaching method.
Construct a new apparatus, Son of X, that preserves all the pedagogical advantages of X but which also features elements that enhance the learning experience of students who do not suffer the cognitive deficit mentioned in 2.
Test the effectiveness of the new apparatus against traditional methods of teaching. Effectiveness is measured not just by the speed at which the student successfully solves various problems, but by the depth of the knowledge imparted.

The recent project focused on stages (3) and (4) of this design process. The area of learning under review was syllogistic logic but it must be emphasized that this was for illustrative purposes only. We suggest that the dog-legged design process, if effective, can be employed in any area of teaching to deliver deep learning.

Deep versus superficial learning

As suggested in the listed points in the section above, an important dimension of the effectiveness of teaching is the facilitating of deeper levels of learning. In this section we consider this and the SOLO taxonomy in particular.

There is a clear intuitive distinction between learning that is 'deep' or rich and learning that is 'surface' or shallow or, perhaps more informatively, superficial. The distinction originates from empirical studies in the 1970's by F.Martin and R.Säljö. 'The surface approach arises from an intention to get the task out of the way with minimum trouble while appearing to meet course requirements.'⁵ A typical realization of this includes rote learning in order to memorize factual content for reproduction, or rules of procedure for application, in an exam, with the aim primarily to maximize grades rather than engage with the subject. Deep learning, such as it happens or is sought by students, by contrast involves engaging more with the meaning of the subject, or at least with the topic, at issue. It aims to determine its rationale or purpose, or how it functions at more fundamental levels, and then to see how its salient facts and its rules for application supervene on the more fundamental. This then will facilitate understanding the facts and rules more thoroughly and effectively for future engagement with the subject. Adopting the alternative surface learning approach, students would rely upon being presented with and then memorizing the facts and rules in their particular salient formulations, rather than making the intellectual links between them and the more fundamental aspects which govern them.⁶

It is important not universally and simply to equate 'deep' with good and 'surface' with bad across all areas of all subjects.⁷ This is because, in some cases, memorizing the rules and facts may be just what should be achieved for getting through an important stage, or getting on top of an aspect, of the subject. So, in the sciences, for instance, objects with different electrical charge attract each other and those with like charge repel each other, whereas all objects (with mass) attract each other gravitationally: that is just the way that it is. Expanding your vocabulary in the first new language which you learn at school is to a significant extent, arguably, just a matter of learning which words are equivalent to those in your native tongue. However, where we as teachers are intending to foster in our students 'proper' understandings of the topics and engagement with the subject, i.e. our curriculum aims to achieve those learning outcomes in our students, we need to ensure that we align our course design, including assessment tasks, and our approach to teaching the course with each other and with producing those outcomes.

It has proved difficult to operationalize the concepts of deep and of surface/shallow/superficial learning in both teaching design and research on learning. However, by way of providing a reasonably firm basis, we shall rely upon the work undertaken by John Biggs. He has produced a more sophisticated taxonomy, employing a number of levels rather than just the two of deep and surface, christened SOLO (Structure of the Observed Learning Outcome).

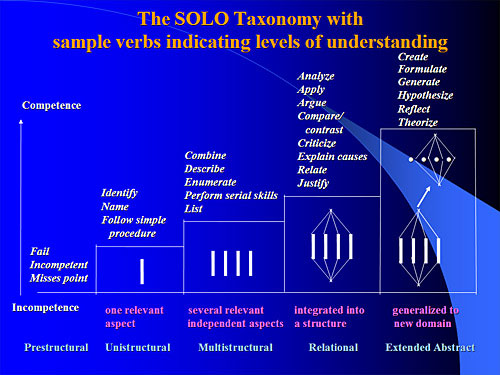
Solo taxonomy image

Figure 1:The SOLO Taxonomy⁸

If students can produce correct answers to questions without understanding fully enough the bases for how they do so, testing their performance in tasks alone does not show us where there is deep understanding and where there is not. Elementary logic, indeed much philosophy, requires the honing of procedural rather than propositional knowledge. Yes, we need to know, depending upon the context, what Plato, Heidegger or Davidson have claimed in their writing but the assessment process in the discipline is geared much more towards the construction of good argument.

Elementary logic, even though dealing in the currency of propositions, especially is a matter of understanding techniques, of achieving know-how. If a student gets (the solution to) a task wrong then we can say that there is some gap in understanding. So it would be fair, and one of the planks of the methodology of the recent project, at least to start with assessing performance at tasks. If students fail at them, we may place them at the 'incompetence', or 'prestructural', level in the SOLO taxonomy illustrated above. It becomes less clear how deep an understanding they have if they succeed with tasks which are based on certain basic rules. Yet we could still maintain that there is important understanding happening (as well as important attainment in the sense of the progress, in marks attained, towards their overall degree programme performance!), even if they reside only at the 'one relevant aspect', or 'unistructural', level. Likewise, with being introduced to a suite of rules, good performance in a test involving all of them would indicate, defeasibly, that they are at the 'several relevant independent aspects', or 'multistructural', level. Ultimately, we would hope that they attain the 'integrated into a structure', or 'relational', level of understanding. The level above that, 'generalized to new domain', or 'extended abstract', would be nominally beyond the introductory level for logic, beyond the how-to-do-it(-well), and into the domain of the philosophy of logic.

We shall return to the question of understanding, in the course of analysing results towards a conclusion of the recent project. We turn now to an account of the development of the project.

Design for the blind: Sylloid

In this section, we recount the evolution of the design of some equipment for teaching elementary logic. The idea of constructing apparatus for reasoning is not new. A distinguished precursor is 'a colorful medieval polymath and sometime poet, rake, and martyr named Raimundus Lullus, or Ramon Lull (ca. 1232-1316). Lull's chief invention was a so-called Ars Magna of encoded, inter-rotating wheels developed in the latter decades of the thirteenth century and articulated in a treatise called the Ars Generalis Ultima'.⁹ The first phase of the recent project consisted of designing a piece of apparatus for the use of blind students; the second phase consisted of designing a new piece of equipment that preserved all the advantages of the apparatus designed for the blind but also incorporated features that took advantage of the full range of perceptual input available to the sighted. This is thus a paradigm case of 'dog-legged' design. The final phase was to test the utility of the teaching apparatus that emerged at the end of this process. Logic is a subject that features in almost every tertiary philosophy curriculum. Syllogisms are a particularly simple type of argument originally investigated by Aristotle, and the theory of syllogisms was the core of logic right up to the last quarter of the nineteenth century. It is still regarded as an important and rather beautiful part of logic, and in recent times has been developed most notably by Fred Sommers. A syllogism consists of two premises and a conclusion, with three noun phrases (or 'terms') each occurring twice over, and each sentence in the syllogism has to be of one of just four allowable types. In the following example, the first premise is of type I, the second premise is of type E and the conclusion is of type O. Type Asentences are of the form 'All Xs are Ys', for example 'All ducks are elephants'. The following particular example is infamous for eliciting conflicting verdicts from people asked to say whether it is valid or invalid:¹⁰

Some tax cheats are parliamentarians.
No blue-eyed people are tax cheats.
Therefore
Some parliamentarians are not blue-eyed.

This alone shows the usefulness of an objective method for determining the correct answer. The validity or invalidity of any syllogism is usually established via algebraic (Boolean) equations or graphically via Venn or Euler diagrams (and makes use of the notion of a set (or class), e.g. the set of parliamentarians corresponding to the common noun 'parliamentarians'). Neither technique is readily available to the severely visually impaired student. It is easy enough to design software such that the student could input a coding of the premises and the conclusion of a syllogism, hit a button and receive instantaneously a correct verdict on that argument's validity. But, of course, the intellectual/ educational value to a user of such a device, visually impaired or not, would be close to zero. This would be an illustration of no better than the 'incompetence', or 'prestructural', level in the SOLO taxonomy illustrated above as regards understanding syllogisms, even if it was satisfying the 'one relevant aspect', or 'unistructural', level as regards how to operate the piece of software. Hence, we can see the need, identified above, to raise the question of just what it is about the nature of syllogisms that makes them a fascinating object of study, to confront questions about the nature of classes (sets) and the relations between them, and questions about what it is to inculcate an understanding of these and of entailment and validity. Such questions are important if one cares about deep learning.¹¹

A Venn diagram (see figure 2) consists of three intersecting circles, each (if your imagination is sufficiently vivid) to be thought of as containing all of the objects, if any, corresponding to a noun-phrase occurring in the syllogism (e.g. if we were representing the above argument Venn-diagrammatically, one circle would 'contain' all the tax cheats, another all the parliamentarians, so that the intersection of these circles contains all the parliamentarians who are tax cheats, if there are indeed any.¹² With three circles intersecting, there are seven distinct areas, as shown in the diagram. There are two basic operations when representing premises on a Venn diagram: (i) shading areas to show that they are empty (contain no objects) and (ii) using a heavy short line (a 'bar') to show the presence of objects where the bar lies.¹³

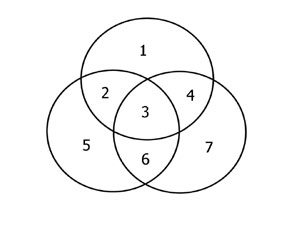
Venn Diagram

Figure 2:Venn diagram

The Venn Diagram consists simply of three intersecting circles (without numbering) and premises are represented by appropriately shading certain areas (to indicate that the class of things represented as being in that area is empty) or by using a solid bar to indicate nonemptiness of the corresponding class.

Jon Barwise and John Etchemendy have done more than most to establish that 'there is no principled distinction between inference formalisms that use text and those that use diagrams. One can have rigorous, logically sound (and complete) formal systems based on diagrams'.¹⁴ But, we ask, why not go up a dimension and produce a physical, highly tactile three dimensional model?

The apparatus (called 'Sylloid') designed by the first author for the use of blind students exchanges the seven areas of a Venn diagram with seven solid tetrahedra. The counterpart to shading an area (in Venn) is to remove a tetrahedron from the core by pulling it off. The counterpart to drawing a bar between two areas (in Venn) is slapping a hinge in the valley between two tetrahedra. If, in the course of representing another premise, one of the tetrahedra on which the hinge is resting is removed, the hinge is folded back, revealing a differently textured surface and remains attached to the tetrahedron that has not been removed. This corresponds, in a regular Venn diagram, to part of a bar being eclipsed when one of the areas in which it lies is declared empty (so the objects that the bar represents as existing must lie in the area where the bar remains, uneclipsed).¹⁵

Sylloid 1 Sylloid 2

Figure 3: Sylloid

Note that, just visible in the picture on the left, the steel buttons are embossed with the braille equivalent of 'X', 'Y' and 'Z'. Note also the textured metal hinge. The device consists essentially of seven tetrahedra that plug into a central core—see the computer deconstruction on the right. Small round magnets are embedded in the exposed faces of the tetrahedra. Sylloid is supplied with an audiotape containing instructions for use.

The task of designing an apparatus for the sight-impaired presented the opportunity not just to produce a device by means of which blind people can test syllogisms for validity or invalidity but to think about what a deep understanding of syllogism involves, and to ensure that it is this kind of understanding that will be promoted, for the user to develop while working with the apparatus. Sylloid was a response to this opportunity and among its prima facie pedagogical advantages over Venn diagrams are the following:

A solid tetrahedron is a slightly more intuitive representation of a set of objects than is a two-dimensional shape. Each tetrahedron in Sylloid visibly represents a discrete set.
In Venn, the intersection (lens) between sets is clearly depicted on the diagram, but the lens has two parts and it is by no means clear what set each part represents. (It is a pedagogically useful exercise to explain to students using Venn just which sets each of the seven areas in turn represent.)
Physically removing a tetrahedron from Sylloid is a much more natural and attractive way of demonstrating the absence of the relevant set of objects than is shading an area in Venn.
The smooth side of the hinge represents the possibility of the presence of objects, the textured side (revealed when one side of the hinge is folded back on the other) represents their actual presence. Venn does not support any counterpart to this useful feature.
There is a strong element of play in Sylloid—pulling out blocks, slapping on hinges etc; Venn is not quite so much fun.
Sylloid is a beautifully crafted object, compared to uninspiring pen and paper.¹⁶

Sight restored: Son of Sylloid

Having, as in the above section, considered the advantages of Sylloid as a device, an intriguing possibility now presents itself. Sylloid is probably a better learning tool than Venn, and if we modified it slightly (e.g. by replacing the brailled letters with regular letters) then it could be used to advantage by sighted students. But why not go one step further and produce a radically new design primarily for the sighted, a Son of Sylloid, that incorporates all the virtues of Sylloid and of Venn and that makes maximum use of the visual sense? A useful first step in this process is to take a hard look at the defects of Sylloid to ensure that they are not transmitted to its heir. These defects are:

It is difficult to get a firm grip on the sloping sides of a tetrahedron made of perspex, especially with clammy hands. Dropping one of the pieces on the floor is obviously a nightmare for a blind user.¹⁷
There is no representation of class intersection in Sylloid. This was pointed out to me by Jon Williamson at a workshop I gave about the present project on 14 October 2009, and it is a major strike against Sylloid, since part of the deep learning of syllogistic logic is understanding the connection (which so excited George Boole, when he discovered it) between the four types of Aristotelian sentence and their counterpart class relations, that can be captured in algebraic equations.
The tetrahedra are of equal size, and this may create the false impression that the classes they represent are equinumerous.
This piece of equipment, the prototype of which was constructed at the Ho Tung Engineering workshop, University of Hong Kong, needs to be built to fine tolerances and is therefore expensive to produce.
It is also very heavy since, at a height of about 25cm, it requires a broad metal base to prevent it toppling over when in use (see figure 3), although an alternative would be to screw it down to the workbench.

The resultant new design, Son of Sylloid, is illustrated in figure 4.

Son of sylloid

Figure 4: Son of Sylloid

The image represents this two-dimensionally but it is a plastic board about 2cm thick. Each of the seven coloured pieces can be removed from the black housing, though typically, when representing the premise of a syllogism, only one or two pieces are removed. The bridging bars are stored as shown (top right); they are used when representing existential premises on the model.

The apparatus is very simple to use, as is illustrated in the pictures below.

First example

Example 1 Example 2

All Ys are Bs FOLLOWED BY All Bs are Rs

This illustrates testing for validity the syllogism:

All humans are mortals
All mortals are arachnophobes
Therefore all humans are arachnophobes.

Use the variables 'Y', 'B' and 'R' as stand-ins for, respectively, the nouns 'human', 'mortal' and 'arachnophobe'. The form of the first premise is 'All Ys are Bs'. Read this 'All Yellows are Blues', then simply remove from the apparatus each piece that has a yellow edge but no blue edge. For the second premise, of the form 'All Bs are Rs', remove any of the remaining pieces that have a blue edge but no red edge. By inspection of the mutilated apparatus that survives, one notes that the only piece with a yellow edge also has a red edge, hence the conclusion 'All Ys are Rs'. In the course of representing the two premises, all those pieces with yellow edges but no red edge were removed. In representing the premises, we eo ipso represented the conclusion, hence the argument is valid. Somewhat metaphorically, a deductively valid argument is often characterised as an argument the conclusion of which is contained in the premises. This notion of containment is made vivid in all three primarily pictorial methods of testing described in this paper, but not in the primarily linguistic methods, Aristotle's original deductions nor their mediaeval refinements nor in Boolean algebra. The invalidity of a syllogistic argument can be immediately read off a diagrammatic representation, for the conclusion is visibly not contained in the premises. Note, for example, that the conclusion 'All arachnophobes are humans' (All Rs are Ys) does NOT follow from the original two premises, for, in its final configuration (right hand figure, above), the mutilated apparatus contains red edged pieces that are not also edged in yellow.

Second example

Some Rs are Ys FOLLOWED BY No Rs are Bs

The first premise is represented, just as in Venn, by placing a bar (signifying the presence of one or more objects) in the area where the red and the yellow quadrilaterals intersect. The bar must therefore lie on each of the two pieces that has a red and yellow edge. Since we do not, at this stage, have information as to which, if any, of the objects signified by the bar is blue and which, if any, is not blue, we use the bar to bridge the two pieces, one of which lies inside the blue quadrilateral, the other outside. The second premise says that there is nothing that is both R and B. Hence, to represent this, we have to remove any piece that has both an R and a B edge. There are two such pieces. There are no objects in those places, so the bridging piece (which shows the presence of objects) must be slid so as to sit on the one available piece, as shown. From the final configuration, we can validly infer 'Some Ys are not Bs'. (We could also validly infer that some Rs are not Bs, but that is trivial, since we already know, from the second premise, that no Rs are Bs.) Note that we cannot validly infer 'Some Bs are not Ys', nor 'Some Bs are Ys'. This is because, although in the final configuration there is a piece with just a blue edge and a piece with a blue and yellow edge, these signify the areas where objects that, respectively, are just B and, respectively, are both B and Y belong, if there are any. The definite presence of one of more objects in an area is indicated by the bridging bar resting on that, and only that, area. As with many linguistically codified instruction manuals, this may sound terribly difficult; it is when you start playing with the apparatus that you realize how utterly simple it is.

We summarise the prima facie advantages of Son of Sylloid over both Sylloid and Venn as methods:

The Son of Sylloid apparatus is visually attractive (certainly if you appreciate Piet Mondriaan!) and its operation makes essential use of colour.
The three main classes and the seven subclasses are represented by pieces of different shapes and sizes in Son of Sylloid, reflecting the differences between the associated classes.
Coloured ridges round the sides of the 'jigsaw' pieces in Son of Sylloid give an immediate indication of the class represented by that piece. Thus a piece edged only in yellow indicates the class that contains objects, if any, that are just Y (i.e. they are not also R or also B).
Son of Sylloid, like Venn but unlike Sylloid, visibly represents class intersection. In Venn, the intersecting circles need to be labelled; in Son of Sylloid intersecting quadrilaterals are identified by the colours of their edges: so the piece edged in red, yellow and blue indicates a class of objects that are R, Y and B
As in Sylloid, the emptiness of a class is signalled by physically removing the relevant piece, but this operation is easier, since hollows have been gouged out to create space for prising fingertips. With Venn, the area would be shaded out but remains ever visible as an area in the midst of the diagram with which you are working.
The operation of showing the presence of objects is enhanced. For instance, in Venn it is a simple line but Sylloid's bar being pitted allows the light to show through from the surface of the class piece underneath, as if more realistically representing actual objects in the class.
The jigsaw pieces are not contiguous (contrast Venn); the world of parliamentarians and tax cheats and blue-eyed people also contains 'all the rest', goats, planets, prime numbers, etc., represented by the housing surrounding al the pieces.
When a bridging bar traverses two pieces, the subsequent removal of one of those pieces removes the support for one side of the bridge and there is just one place for it to go – onto the remaining piece. This is a more natural operation than the eclipsing of a line bar by a shaded area as in Venn, since the half of the line on the paper, as well as the shaded (empty set) area covering it, remain as strong traces on your paper.
When representing in Venn a type A sentence of the form 'All Bs are Ys', one first has to paraphrase this, mentally at least, as 'There is nothing that is B that is not Y' and, accordingly shade as empty the area of the B-circle lying outside the Y-circle. Arguably, understanding why 'All Bs are Ys' is equivalent to 'There is nothing that is B that is not Y' is part of the deep learning of syllogism. A lot of students find this mental manipulation difficult, and get it wrong. With Son of Sylloid, we anticipate that the required mental manipulation is facilitated more readily and successfully. You see a B that is not Y (e.g. a piece with a blue edge but not a yellow) and you take it out; then you see another piece with a blue edge but not a yellow, and you take it out. Removing the pieces is functionally equivalent to the shading of two areas in Venn. We declare that Son of Sylloid and Venn are functionally isomorphic but the former is more kinaesthetic on top of being visual. So we anticipate that doing this operation in two stages, with demonstrative identification of the physically distinct pieces to take out by more pronounced physical action, would be a more emphatic action than shading on paper and so ultimately more intuitive to carry out correctly, reinforcing the deep learning.
As illustrated in the two examples of argument-testing above, the process of testing in Son of Sylloid is quicker, easier and more fun than in either Venn or Sylloid, BUT it is so only once you have got used to it. In his original proposal, the first author badly underestimated the time it would take a student new to the subject to learn about syllogisms and how to test them for validity. It was simply unrealistic to suppose that this could be done in one hour.
Unlike Venn, Son of Sylloid is re-usable; unlike Sylloid, it is light, not cumbersome, cheap and easy to produce.

There is certainly a disadvantage of Son of Sylloid. Since, in Sylloid (and in Son of Sylloid), pieces are physically removed from the apparatus, compared with Venn, it is difficult (unless you have an exceptionally good memory) to remember what classes the removed pieces represent. This defect can be remedied in a variety of ways at a cost of making the apparatus a little more expensive, but this defect (if it is one) is so minor that it is not worth bothering about. Another design defect, noticed after the apparatus was constructed, was that, although the surface under the seven pieces should be black (so that the removal of a piece reveals a black void) the space surrounding and flowing between the seven pieces should be some other colour, representing everything in the world, except the Ys, Bs and Rs.

If the conjecture that Son of Sylloid is more effective than traditional methods for non-visually impaired learners proves correct, then the design methodology outlined here is likely to be applicable right across the board and will have a profound impact on the design of all kinds of teaching material. We have used, merely as an illustration, the teaching of a very narrow aspect of logic. We turn now to an account of how we went about empirically testing the usefulness of the new device.

The testing

For the empirical phase of the recent project, we devised a simple experiment to test the relative effectiveness of three separate approaches to teaching syllogism. The status of the testing is highly exploratory, piloting the prospects of a statistically more rigorous test using more people in more locations. The experimental plan passed successfully through the process of consideration of the UELT Research Ethics Committee at the University of Kent. The three approaches are, respectively, by means of Boolean algebra, of Venn diagrams and of Son of Sylloid. Students acting as participants in the experiment were set a brief paper test. There was a pre-test (on 3 March 2010) with eight philosophy students and two lecturers, to gauge whether the test paper was comprehensible and usable in the relevant context and to inform the subsequent approach.

The pilot testing proper was carried out on 29 March with participants supposedly innocent of the ins and out of methods of logic and especially of the three teaching methods. They were sixth form school pupils taking their A levels that year. They were assembled in three groups, instructed separately respectively in one of the three methods and not the other two, and given the paper test correspondingly. The test (with the same three syllogisms for all¹⁸) was as follows:

Check your knowledge of syllogisms

[One of the three following rubrics displayed, according to which group they were in:]

Test the following arguments for validity using Boolean algebra. Show your working on the right.
Test the following arguments for validity using Venn Diagrams. Show your working on the right.
Test the following arguments for validity using Son of Sylloid.

No bees are wasps.
Some wasps are carnivores.
Therefore
Some carnivores are not bees.
Answer: VALID / INVALID (delete whichever does not apply)

All karts are vehicles.
Some vehicles are not toys.
Therefore
Some karts are toys.
Answer: VALID / INVALID (delete whichever does not apply)

Some roads are links between famous cities.
Some links between famous cities are motorways.
Therefore
Some roads are motorways.
Answer: VALID / INVALID (delete whichever does not apply)

There were seven test papers submitted having used Boolean, seven test papers submitted having used Venn, six test papers submitted having used Son of Sylloid. As regards the three questions per participant asking them to test for validity:

The Boolean group collectively scored 9 correct answers out of a possible 21.
The Venn group collectively scored 14 correct answers out of a possible 21.
The Son of Sylloid group collectively scored 9 correct answers out of a possible 18.

It would appear that the Venn Diagram method is most effective, if by that we mean precipitating the correct answers more readily. A major caveat is that there is evidence that the students were familiar with Venn Diagrams in another context, since some who were instructed to use one of the other two methods used Venn diagrams in working on their paper sheets. So the Venn group may have had a head start in a certain familiarity in this method.

Conclusions

What we can conclude with confidence from the testing is that we cannot conclude that Son of Sylloid clearly has potential for more effective learning but, on the other hand, neither is it clearly inhibiting learning. There is a clear case, then, if we wish to determine which method is most effective, for rolling out a larger funded project comparatively testing the teaching methods more rigorously, using a much larger population of participants over a range of ages, geographical areas and types of school.

By way of some evaluation of the testing component of the project, we recognize that there should have been more direction by the tutor as regards appropriate presentation of working on the test papers; furthermore, there could usefully have been more questions for participants to answer. Also, there should have been more time set aside generally for preparing the participants for what they had to do (see point 10 in the list of 'advantages of Son of Sylloid over both Sylloid and Venn'). A more subtle problem with the test may have been that, even if the 3-D manipulations are intuitive for some, the mindset encouraged is still one of language and notation. This is, in the first place, because there is a sheet of paper and answers were to be recorded on the sheet. The questions were asking the students to state whether an argument written is valid or invalid. But could a depiction of the visual end result of manipulation of Son of Sylloid be the 'answer' (even if that would also be translatable into language) to certain other types of test questions, for instance asking what is the conclusion to a set of premises?. Finally, a larger project would usefully include a significant qualitative component to gauge what the participants think they are doing while they are doing it, to uncover what thought processes triggered by what situations might be crucial in their learning.

As indicated in the previous sentence above, we ought to turn attention back to the question of proper understanding, the deep versus surface learning matter and what these involve in their nuances. Overall, this project has produced by way of findings, rather than simple answers to simple questions, instead further useful questions for further enquiry. If a rigorous test still shows the Venn diagrams method precipitating more correct responses, then we could speculate that 2-D diagrams are more intuitive than 3-D object manipulation, perhaps since secondary school age pupils are no longer infants learning how to use their bodies by means of moveable objects and have developed to become more used to writing and drawing meaningfully. What would this tell us about understanding, however? Perhaps knowing intuitively how to proceed without having to puzzle about it is reasonably deep understanding. Such a position would reinforce our point above that the two stages of the SOLO taxonomy which are deeper than incompetent/ prestructural, i.e. the unistructural and multistructural levels, circumscribe adequate learning at this level.

On the other hand, Wittgenstein's illustration in Philosophical Investigations of knowing how to proceed concerns understanding how a quasi-linguistic formula works and so perhaps getting the answers right on the Boolean method is circumscribed even more thoroughly by these levels of SOLO. We might say that, except that we notice that the performance of this group in the test was the worst. This might be because more in this group missed the point and did not understand. If so, this might be, in turn, be because the method is simply not as intuitive for most humans, or because it is less good at encapsulating what syllogism is 'about'. Or, by contrast, arguably, perhaps with the linguistic/ symbolic notation, you have to understand more deeply (more relationally in SOLO terms) what it is about before you can put your answer together. Whereas for Venn diagrams it may be more a matter of following a sequence of instructions, which produces the answer quasi-automatically, such that deeper understanding would be less a factor in working using this method. Paradoxically, the more a group seems to have struggled to get the correct answers, given the equal (and equally short) tuition time, the more it may be a matter of requiring deeper understanding to get anywhere, and the more automatic methods would produce the correct answers more readily. This relates to a (contestable) point made above about the learning of logic being a matter of acquiring techniques. After playing with it for a while, Son of Sylloid does become very easy to use, so assessment of its true efficacy would require a much extended testing time.

Our conclusion is becoming increasingly hesitant and speculative but the point is to encourage further discussion of what we want to be happening for deeper understanding in our students. We need to consider whether it can practically possibly be the same for all students, who between them may display differences in learning aptitude (for whatever reason, an intelligence differential, or upbringing- fostered prejudice, etc.). Insofar as they have these differences they demand sensitivity from teachers in the interests of fairness to them as regards the appropriate method of teaching, with one method unlikely to suit all. This is then in the interests of a call for consideration of Son of Sylloid as one such method for teaching syllogism and for production and experimentation of further variations of the tool, and, indeed, whole new methods.¹⁹

Perhaps the repeated usage of the more mechanical device would facilitate deeper understanding than linear notation can: you keep doing it and then how it works, what it means, 'clicks' with you. As reported above (in the list of 'advantages of Son of Sylloid over both Sylloid and Venn' point 9), some moves in the manipulation are not so intuitive to new learners: and consider the first example illustrating Son of Sylloid, above; the conclusion to the example is 'All B's are R's' but you cannot read that alone off the diagram, as opposed to 'Some Y's are R's', for instance. Rather than it being too obvious initially for them, forcing learners to have to think about what they are doing and what it means may be our most promising clue to the fostering of the deeper understanding we seek.

References

Atherton, J. S., Learning and Teaching; SOLO taxonomy [On-line] UK, 2010; available at http://www.learningandteaching.info/learning/solo.htm , date last modified 10th February 2010. Accessed: 5th October 2010.

Barwise, Jon and Etchemendy, John, 'Heterogeneous Logic', in Glasgow, J., Hari Narayanan, N. & Chandrasekaran, B. (eds), Diagrammatic Reasoning: Cognitive and Computational Perspectives (Cambridge, MA: AAAI Press/The MIT Press, 1995) pp.209-232.

Biggs, John, Teaching for Quality Learning at University: What the Student Does, 2nd edition (Maidenhead, UK: The Society for Research into Higher Education & Open University Press, 2003) xii+309pp.

Fleetham, Mike, Multiple Intelligences in Practice (London: Continuum Education, 2006).

Gardner, Howard, Frames of Mind: The Theory of Multiple Intelligences, 20th anniversary edition (New York, NY: BasicBooks, 2004) xxxii+440 pp.

Gardner, Howard, 'Multiple Intelligences after Twenty Years' (Paper presented at the American Educational Research Association, Chicago, Illinois, April 21 2003): http://www.pz.harvard.edu/PIs/HG_MI_after_20_years.pdf . Accessed: 5th October 2010.

Goldstein, Laurence, 'Making a Virtue of Necessity in the Teaching of the Blind', Journal of Teaching Academic Survival Skills, 1, (1999) pp. 28-39.

Goldstein, Laurence and Liu, N.F., 'An Integrated Approach to the Design of an Immersion Program', TESOL Quarterly, 28/4, (Winter 1994) pp.705-725.

Nowviskie, Bethany Paige, Speculative Computing: Instruments for Interpretative Scholarship (doctoral dissertation, University of Virginia Department of English, May 2004), 328pp; available at: http://www2.iath.virginia.edu/bpn2f/diss/dissertation.pdf
Accessed: 5th October 2010.

Searle, John R., 'Is the brain's mind a computer program?', Scientific American, (January 1990) pp. 20-25.

White, John, 'Illusory Intelligences?', Journal of Philosophy of Education, 42/3-4, (2008) pp. 611-630.

Endnotes

We would also like to thank Kevin Smith of the Kent School of Architecture Workshop for building six Sons of Sylloid and for suggesting some refinements of the design. For help with diagrams and photographs, we thank, respectively, Justin Mahone and Charles Young and, for helping to set up the instruction/testing sessions at Simon Langton School for Boys, Charlie Artingstoll.
From the blurb for Mike Fleetham's useful and amusing book: Fleetham, Mike, Multiple Intelligences in Practice (London: Continuum Education, 2006).
Goldstein, Laurence and Liu, N.F., 'An Integrated Approach to the Design of an Immersion Program', TESOL Quarterly, 28/4, (Winter 1994) pp. 705-725.
For further synoptic discussion of Gardner, see White, who is supportive of the idea that individuals manifest intelligence in different ways and that MI can be used heuristically, or figuratively at least, as part of a good approach to teaching: White, John, 'Illusory Intelligences?', Journal of Philosophy of Education, 42/3-4, (2008) pp. 611-630.
Biggs, John, Teaching for Quality Learning at University: What the Student Does, 2nd edition (Maidenhead, UK: The Society for Research into Higher Education & Open University Press, 2003) xii+309pp., p14.
This discussion may already remind the reader about John Searle (1990) and his 'Chinese Room' thought-experiment. In his envisaged situation, someone has a set of instructions in English for receiving instructions or questions in Chinese and for responding to them in Chinese. Searle argues that the correct output response (as in the writing) is not a sufficient condition for understanding, in the sense of this person understanding Chinese as a language. Can testing for validity, or otherwise following the procedural rules of deduction, be like this for some students who nonetheless get the right answers?
Arguably Biggs (ibid., p.31) himself succumbs to this facile mantra.
This representative diagram is available on John Biggs's website and we reproduce the image with his permission: http://www.johnbiggs.com.au/solo_graph.html. The taxonomy is explained in Biggs (ibid., chapter 3, including another version of this diagram on p. 48). Examples of other sites which introduce the taxonomy: http://www.adelaide.edu.au/clpd/assessment/design/; and Atherton (2010). Websites accessed: 5th October 2010.
Nowviskie, Bethany Paige, Speculative Computing: Instruments for Interpretative Scholarship (doctoral dissertation, University of Virginia Department of English, May 2004), pp. 328; available at http://www2.iath.virginia.edu/bpn2f/diss/dissertation.pdf Accessed: 5th October 2010.
Logicians are not concerned primarily with the truth or falsity of the propositions occurring in an argument, but with whether or not the conclusion follows from (aliter: is entailed by) the premises.
The underlying pedagogical theory, and a technical discussion of the particular case of logic learning has been disseminated in Goldstein, Laurence, 'Making a Virtue of Necessity in the Teaching of the Blind', Journal of Teaching Academic Survival Skills, 1, (1999), pp. 28-39.
As Private Eye would say: 'Shurely not'!
Interestingly, the invention of the bar was due not to Venn but to Charles Sanders Peirce.
Barwise, Jon and Etchemendy, John, 'Heterogeneous Logic', in Glasgow,J., Hari Narayanan, N. & Chandrasekaran, B. (eds), Diagrammatic Reasoning: Cognitive and Computational Perspectives (Cambridge, MA: AAAI Press/The MIT Press, 1995), pp.209-232, p214.
The idea of switching from traditional media has, to some extent, been anticipated by Barwise and Etchemendy in their logic software 'Turing's World' and 'Tarski's World', which makes use of 3-D graphic techniques for inference.
One can thus take advantage of the Hawthorne effect, i.e. the participants may respond just to the knowledge that care is being taken to satisfy their needs, that they are at the centre of an innovation aiming to assist them: whether or not what you do for them inherently produces a good effect, the fact that you have taken trouble to do this may improve their performance.
…and causing the wrong sort of 'impact', perhaps… This hazard would have been apparent, at the outset, to a competent designer, but was not to yours truly, first author!
There was a bit more to the test paper. The following was extra working for those finishing the main questions quickly, and an additional but not systematic check on their understanding of logic:
Examine the following personality sketch:
Bill is 34 years old. He is intelligent, but unimaginative, compulsive and generally lifeless. In school, he was strong in mathematics but weak in social studies and humanities.
Which statement is more probable:
A. Bill is an accountant that plays jazz for a hobby, or
B. Bill plays jazz for a hobby?
Answer:
What is it for premises to entail a conclusion?
Answer:
Explain the intersection between two sets.
Answer:
The recent project seeks as a coda to put in train workshops for, for example, secondary school teachers where they learn the dog-legged design technique and come back in, say, 4-6 weeks with innovatory materials of their own. The first author ran a pilot for such workshops at the University of Kent on 21st September 2010, the audience consisting mainly of language teachers. The two pieces of logic apparatus described above were used as illustration. Teachers were so enthused that they volunteered to return with innovatory language-teaching materials inspired by the dog-legged approach to design. This was an unexpected, but very gratifying, response.

Return to vol. 10 no. 1 index page

This page was originally on the website of The Subject Centre for Philosophical and Religious Studies. It was transfered here following the closure of the Subject Centre at the end of 2011.