Teaching and Learning > DISCOURSE
The Case for Teaching Syllogistic Logic to Philosophy Students
Author: Brendan Larvor
Journal Title: Discourse
ISSN:
ISSN-L: 1741-4164
Volume: 4
Number: 1
Start page: 130
End page: 136
Return to vol. 4 no. 1 index page
The case for not teaching syllogistic logic is easy to state: syllogistic logic is a superseded theory. Teaching Aristotle’s logic in the presence of modern mathematical logic is not quite as perverse as teaching his physics in the presence of modern physics, because syllogistic logic successfully identifies those valid arguments that fall within its scope (but as it is a monadic logic, its scope is rather narrow). Aristotle’s physics, on the other hand, is unsuccessful even within its proper bounds. Nevertheless, syllogistic logic has been overtaken by mathematical, polyadic logics, and some motivation must be given for according it a place in an overcrowded syllabus.
This demand naturally raises the question of why we teach logic to philosophy students at all. Many of the familiar reasons do not tell strongly for or against syllogistic logic in comparison with modern logic. For example, it is important that students should get hold of the idea of a valid argument as such—but you can teach this notion with any logical system, ancient or modern. We should like philosophy students to understand that some arguments owe their validity solely to their logical forms—but again, you can teach this using any system of formal logic, including syllogistic. What is more, one can teach these notions in a single lesson, so what is the rest of the module for? There is, in addition, the rather dubious claim that studying logic makes one a more careful thinker. Insofar as this is true, I am inclined to think that almost any rigorous discipline will achieve the same. Learning foreign languages in a relatively formal fashion probably does as much to improve students’ analytical nous as formal logic, if not more (what better way to develop a nose for equivocation than regularly translating between natural languages?). In any case, when we meet bad arguments in real life, the fallacies are almost never those errors of reasoning such as quantifier-shift that mathematical logic is uniquely equipped to expose, nor does one often find examples of illicit process or undistributed middle terms in newspaper columns. Informal fallacies such as equivocation, hasty induction or ad hominem attack are far more common, which is why those institutions that are seriously worried about their students’ analytical acumen tend to put on critical thinking courses rather than courses in formal logic. In short, the familiar reasons for teaching logic do not especially favour modern logic over the ancient. Indeed, syllogistic logic may be a better vehicle for teaching general notions such as validity and formality simply because many students find it easier than mathematical logic.
One reason for teaching modern mathematical logic rather than syllogistic logic is to prepare students to participate in those philosophical research programmes that depend on it. It is, of course, one of the aims of an undergraduate degree to prepare students for postgraduate study, but not the only one. When philosophy is widely studied within modular schemes, only a tiny minority of philosophy undergraduates progresses to postgraduate work, and of these a yet smaller minority works on the sort of philosophy that demands mastery of modern logic. So this is only a weak reason for subjecting all philosophy undergraduates to extensive and possibly compulsory mathematical logic.
So the case against teaching syllogistic logic is weak, but to justify making time for syllogistic in the syllabus we need some positive reasons for teaching it. These come in two groups: there are the benefits that arise from teaching syllogistic logic on its own, and there are the benefits that arise from the contrast made available by teaching syllogistic and mathematical logic together. In the first group, there is the fact that the categorical sentences of syllogistic logic look like sentences of natural language. Those students who panic at the sight of a blackboard covered in mathematical symbols find syllogistic logic less intimidating. The force of this point really depends on the student body; where philosophy is taught as part of a humanities scheme, many of the students will have deliberately done no mathematics since GCSE. Recent years have seen a decline in mathematics in schools and a flight from most of the numerate disciplines in universities. Philosophers should take account of this. As mentioned already, syllogistic logic offers a way to achieve most of the general goals of logic teaching listed above with those students who simply would not cope with mathematical logic.
Second, syllogistic offers two tests for validity: Venn diagrams and the theory of distribution. Having two tests for validity makes vivid and concrete the distinction between the concept of validity itself, and the means of testing for it. In mathematical logic, these can be obscured as students often learn by rote a technique for testing for validity, without really grasping the notion itself (they might, of course, learn more than one technique in mathematical logic too, but this is a much greater undertaking than learning both syllogistic techniques).
A third motivation for teaching syllogistic logic arises from the historical character of philosophical training. Philosophy students are taught largely through the classic texts of the discipline, many of which predate mathematical logic. Those great dead philosophers who wrote before Frege and who placed logic near the centre of their philosophical projects are difficult to read unless one appreciates the shortcomings of the logic with which they were equipped. Consider, for example, Leibniz’s definition of truth, or Kant’s definition of analyticity. These definitions were supposed to encompass the whole of rational discourse, but they are cast in the impoverished logic of their times and are therefore restricted to its narrow scope (categorical statements and simple conditionals). This leaves our two historical rationalists struggling to get their basic philosophical machinery to work. These struggles make the texts less clear than they might otherwise have been, and consequently, the relevant passages are barely intelligible unless one learns a bit of syllogistic logic first. If we are serious about getting students to read primary sources, we have to give them the means to make sense of them. For early modern rationalists, amongst others, that includes syllogistic logic.
Further motivations appear when we consider the contrast between syllogistic and mathematical logics. With both kinds of logic in view, it is easy to raise the question of the existential import of universally-quantified sentences. Syllogistic logic usually takes it that if all S are P then there must be some Ss, while may be true even if there is no x such that Sx. In other words, syllogistic logic assumes that universally-quantified sentences do have existential import, while mathematical logic assumes that they do not. Natural-language examples can push one’s intuitions either way, and this naturally leads to a discussion about the relation between ragged, unsystematic natural languages and perfectly tidy formal languages. This example helps students to see that the tidiness is achieved at the cost of some arbitrariness and insensitivity to particular cases.
One of the weaknesses of many undergraduate modules in mathematical logic is that students are presented with just one logical system, and go away thinking that there is only one. There is no prospect of teaching so-called deviant logics as a matter of course, so students may imagine that the ‘correct’ analysis of the logical form of a sentence is unproblematic and philosophically uninteresting. At least if they learn syllogistic and mathematical logics together, they can see that there may be more than one way to analyse a given sentence. Tutors can use this to remove some of the authoritarian arbitrariness of logic teaching. To return to the example of existential import, some students will feel inclined to agree with Aristotle. We teachers of syllogistic logic don’t have to say, “I know you feel that makes sense only if there are some Ss, but in this system it is true when there is no S, and this is the system you’ll be examined on, so shut up”. Of course, no-one would say anything quite like that, but the effect of teaching mathematical logic only can be the same. If students do not see their intuitions reflected anywhere in the syllabus, they become alienated from it. And for a teacher trying to make the conventions of mathematical logic seem plausible, it is tempting to brush unhelpful intuitions aside (as kindly as possible, needless to say). With syllogistic in view, we can say, “Some great logicians of the past agreed with you about this, and that is why their system was set up thus. But the cost of assuming existential import for universally-quantified sentences is….” What were unhelpful intuitions are now the basis for a meta-logical discussion.
Whenever possible, logic teachers should find and discuss respectable logicians who share the intuitions commonly experienced by students. Otherwise students may feel that their objections to some of the arbitrariness of logical theory have been ignored rather than answered. To conclude, let me give another example of this. The traditional square of oppositions divides categorical sentences thus:

This can conflict with natural intuitions because for good Gricean reasons, ‘Some S are P’ normally entails that some S are not P. Otherwise, one would say ‘All S are P’, or ‘As far as we know, all S are P’. It may be significant here that natural languages do not have single words to refer to the bottom right-hand corner, the particular negative. Perhaps instead of a square of opposition there should be a triangle of contraries:
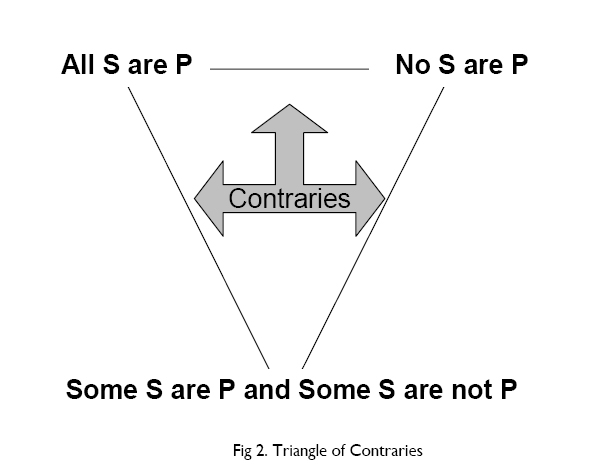
This though is a rather impoverished basis for logic. Instead, the French logician Robert Blanché proposed a hexagon of oppositions, formed from the traditional square by adding ‘Some S are P and some S are not P’ at the bottom and ‘All S are P or No S are P’ at the top (‘Sur l’opposition des concepts’ Theoria vol. 19 (1953) pp. 89 130). There is no need to explore this idea in detail; a mention of it will reassure students that their natural intuitions are not silly or evidence of a lack of talent for logic. On the contrary, the student who spontaneously sniffs out the oddness of saying ‘Some S are P’ and meaning ‘Some, possibly all, S are P’ is to be praised.
Finally, let me offer some evidence that syllogistic logic is intellectually interesting as well as pedagogically and historically useful. Another French logician, Jean-Yves Béziau, has taken Blanché’s hexagonal model and generalised it to include modal operators and non-standard forms of negation (para-consistent and para-complete). This gives him enough hexagons to create a stellar dodecahedron of oppositions. This is tantamount to a representation theorem for modal logic in solid geometry. As a result, relationships between modal logics can be modelled using coloured sticks and blobs of putty.
Return to vol. 4 no. 1 index page
This page was originally on the website of The Subject Centre for Philosophical and Religious Studies. It was transfered here following the closure of the Subject Centre at the end of 2011.